Equação matemática pode ajudar na erradicação de epidemias

Fórmula pode ajudar as autoridades de saúde a definir estratégias para o combate às enfermidades.
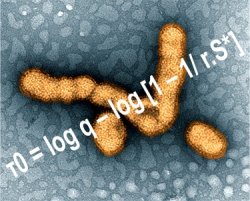
[Imagem: Wikimedia]

Matemática contra epidemias

Em termos estatísticos, duas variáveis são consideradas críticas para se obter êxito no enfrentamento de uma epidemia: o tempo de detecção da doença e o tempo de isolamento dos indivíduos afetados.

Matemáticos brasileiros e alemães desenvolveram agora uma equação que permite calcular o valor ótimo para o tempo de detecção.

"Partimos de um modelo clássico da epidemiologia, o SIS (Susceptible - Infectious - Susceptible), que descreve infecções como as causadas pelos vírus da influenza, que não conferem imunização duradoura às pessoas que as contraem e se recuperam", explica Tiago Pereira, professor da USP em São Carlos.

"Os indivíduos são suscetíveis antes, infectados durante e suscetíveis depois. Esse modelo considera, portanto, apenas dois estados: ou as pessoas estão saudáveis ou as pessoas estão doentes. Nossa ideia foi agregar um terceiro estado: os indivíduos isolados. No novo modelo, os indivíduos infectados são identificados após um certo tempo e isolados para o tratamento", acrescentou.

Equação das epidemias

Os matemáticos chegaram à seguinte equação:

τ0 é o tempo de detecção e diagnóstico da doença; q, a fração da população infectada identificada; r, o número de pessoas que podem ser infectadas se tiverem contato com um indivíduo já infectado (esse número varia de acordo com a enfermidade); e S*, a fração de indivíduos saudáveis na população.

"Se a doença for diagnosticada em tempo menor ou igual a τ0, o isolamento será sempre efetivo. Mas, se a doença for diagnosticada em tempo maior do que τ0, o sucesso na erradicação passará a depender criticamente do tempo de isolamento", explicou Tiago.

Assumindo que tivesse sido possível identificar todos os indivíduos infectados (q = 1) e controlar completamente a doença (S* = 1), os pesquisadores obtiveram para algumas epidemias analisadas os seguintes tempos críticos de detecção:

• Gripes sazonais: = 5,4 dias
• Gripe Espanhola em 1917: 2,1 dias
• Ebola em 2014 (Guiné e Libéria): 3,3 dias
• Ebola em 2014 (Serra Leoa): 1,6 dia

Restrições

Nesse tipo de cálculo, a população de um país é considerada um conjunto fechado - isto é, sem entradas e saídas de indivíduos. É claro que se trata de uma situação ideal, que não se aplica ao quadro real da epidemia de H1N1 no Brasil, por exemplo, onde as fronteiras estão abertas e a doença já se encontra disseminada em uma grande parcela da população.

Mas a equação pode ajudar as autoridades de saúde a definir estratégias para o enfrentamento de epidemias futuras.